PyTorch 线性回归

发表于 | 分类于 | 评论数： | 阅读次数：
字数统计：606 字 | 阅读时长：3 分钟

线性回归

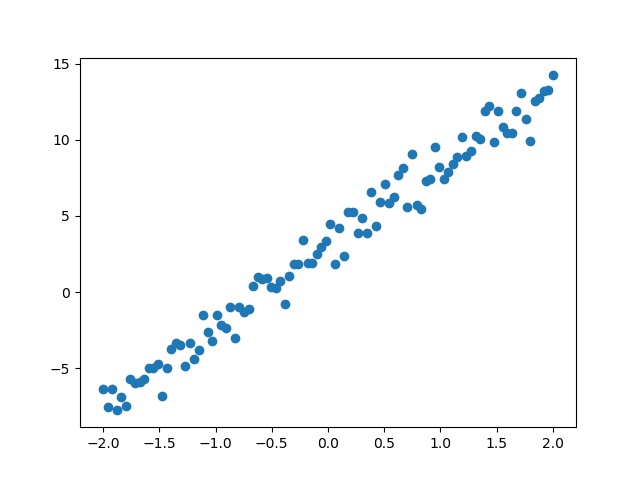
线性回归是机器学习中最基本的模型，也是必须掌握的模型，其中涉及到最小二乘法，均方误差等，目的就是求得一条直线拟合一些点，首先生成如下图片的点，下面会用pytorch代码实现直线的拟合。

img

PyTorch代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
import torch
import numpy as np
import torch.nn.functional as F
import matplotlib.pyplot as plt

# y = 5.2x+3  一元线性函数，斜率 5.2，截距3
true_w = 5.2
true_b = 3
x = torch.unsqueeze(torch.linspace(-2, 2, 100), dim=1)
y = true_w*x + true_b

# 为y值增加高斯噪音，弄得像随机的，等下拟合出一条直线来回归这些点
y = y + torch.randn(x.size()) 

# 打印散点图
plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()

# plt更新
plt.ion()
plt.show()

# 定义一个线性回归的类，继承于Module
class LinearRegression(torch.nn.Module):
    def __init__(self):
        super(LinearRegression, self).__init__()
        self.linear = torch.nn.Linear(1, 1)  # 线性模型，一个输入，一个输出
    
    def forward(self, x):
        return self.linear(x)
    
model = LinearRegression()

# 均方误差损失
loss_function = torch.nn.MSELoss()

# 随机梯度下降，学习率 1e-3
optimizer = torch.optim.SGD(model.parameters(), lr=1e-3)

# 另外一个优化方法 Adam
#optimizer = torch.optim.Adam(model.parameters(), lr=2e-2)

# 迭代次数 2000
epochs_num = 2000

for epoch in range(epochs_num):
    # forward
    out = model(x)
    loss = loss_function(out, y)
    
    # backward
    optimizer.zero_grad()  # 梯度还原为零
    loss.backward()        # 反向传播
    optimizer.step()       # 更新参数
    
    if (epoch+1) % 20 == 0:
        # print('Epoch[{}/{}], loss: {:.6f}'.format(epoch+1,epochs_num,loss.data.item()))
        plt.cla()
        plt.scatter(x.data.numpy(), y.data.numpy())
        plt.plot(x.data.numpy(), out.data.numpy(), 'r-', lw=5)
        plt.text(-2, 12, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size':15, 'color':'red'})
        plt.pause(0.1)

plt.ioff()
plt.show()

可以调整学习率、迭代次数、优化方法，看看不同的调整，会有什么不同的结果

  • 学习率太小，可能导致迭代速度过慢，迭代次数结束后，损失还很大
  • 学习率太大，可能导致无法收敛，并出现振荡，迭代结束后，损失依然大
  • Adam使用的学习率与SDG使用的学习率并不一定会一样

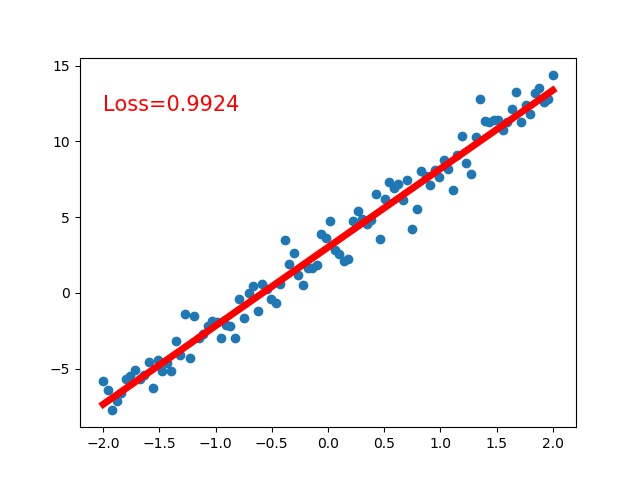
最后拟合出来的图像如下图：

img

代码也可以查看我的GitHub仓库LinearRegression，如有错误，欢迎指出。